Maybe I never learned this or maybe I forgot but while reading Prime Obsession I came across a concept that blew my mind. We all learn about infinite series and how some converge (think 1 + ½ + ¼ + .. = 2) and some diverge (1 + ½ + ⅓ + ¼ + ..) but it turns out that not all convergent series are the same. The same numbers, added in a different order, can lead to a different resulting sum. These series are called conditionally convergent. This is incredible since I always assumed that addition was commutative but it turns out even fundamental ideas are violated when dealing with infinite sums. I still can’t wrap my mind around how this makes any sense but the math doesn’t lie. The example below is from the book but I’d love to see others so I can continue wrapping my head around it. I’ve been out of school for a while now but this discovery brings me back.
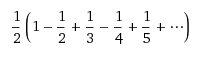
The alternating harmonic series.
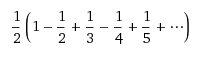
Move the terms around so we have the 1/n and 1/(2n) terms next to one another, but keep those where n is a multiple of 4 alone.
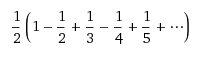
Group these 1/n and 1/(2n) pairs together.
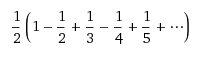
Simplify these 1/n and 1/(2n) pairs.
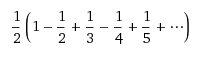
Factor out 1/2 from the series and we have 1/2 of the original series. The sum of the alternating harmonic series is ln(2) but by changing the order around we can have it equal to ln(2)/2. That's amazing.
