As a follow up to my previous post, I modified my Sierpinski generation code to allow specifying the number of sides and the distance ratio for each iteration of the loop. The Sierpinski triangle can be generated with 3 sides and a distance ratio of 0.5. Increasing the number of sides and decreasing the ratio leads to some interesting patterns - it looks as if for a given N, we get N shapes each consisting of N shapes. I suspect this is a fractal pattern - similar to the triangle - but it’s difficult to confirm given a fixed screen resolution. I’d love to know what’s going on here and whether there’s a relationship between the number of sides and the distance ratio.

• 

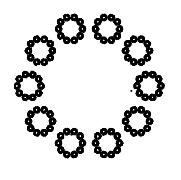
  N = 4, ratio = 0.4

• 

  N = 10, ratio = 0.2